Przykłady procedur w asemblerze ST7 realizujących podstawowe działania arytmetyczne
Podstawą działań wielu programów są różne operacje arytmetyczne wykonywane czy to na zmiennych wejściowych, czy to na zmiennych wewnętrznych. W tym artykule opiszę propozycje procedur wykonujących podstawowe działania arytmetyczne takie jak: dodawanie, odejmowanie, mnożenie i dzielenie, porównanie liczb oraz konwersja liczb binarnych na dziesiętne. Artykuł napisano na podstawie noty aplikacyjne firmy STMicroelectronics „ST7 Math Utility Routines“. Procedury są dokładnie opisane a ich algorytmy działania przdstawiono w formir rysunków i dlatego łatwo można je zaadoptować również dla innych mikrokontrolerów.
Dzielenie całkowite dwóch liczb 1-bajtowych bez znaku
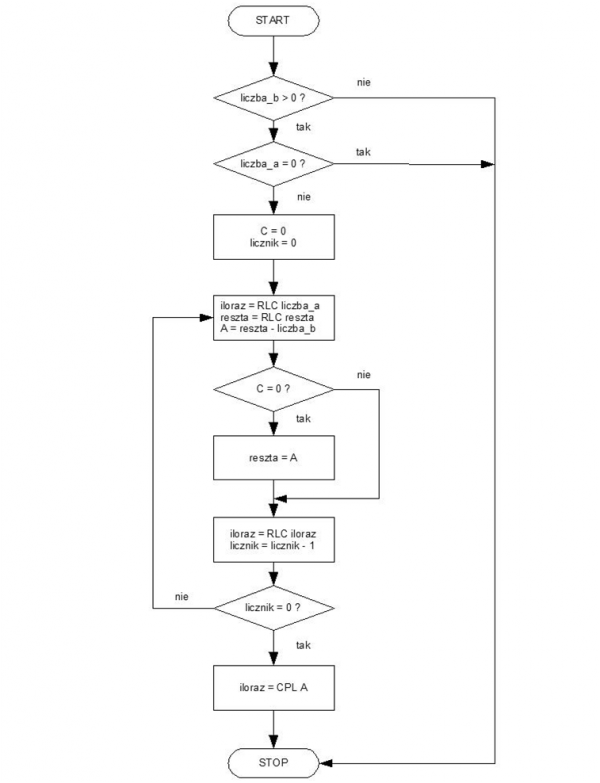
Na rysunku 1 przedstawiono schemat podprogramu dzielenia dwóch liczb 1-bajtowych zamieszczonego na listingu 1. Obie liczby muszą być większe od 0. Funkcja nie sygnalizuje faktu błędnej operacji dzielenia, to jest dzielenia przez 0. W przypadku, gdy dzielna lub dzielnik nie są właściwe, wynikiem działania jest 0 i funkcja kończy pracę. Wykonywana jest operacja dzielenia liczb całkowitych liczba_a / liczba_b. Rezultatem działania jest wynik zapamiętany w zmiennych iloraz i reszta.
Rysunek 1. Schemat działania podprogramu dzielenia liczb 1-bajtowych.
Listing 1. Podprogram dzielenia dwóch liczb 1-bajtowych
;*******************************************************
;dzielenie liczba_a / liczba_b
;argumenty:
; - liczba_a = dzielną
; - liczba_b = dzielnik
; - liczba_a i liczba_b ≠ 0
; - cnt (jako licznik działań)
;rezultaty:
; - iloraz zawiera część całkowitą z ilorazu liczb
; - reszta zawiera resztę z dzielenia
;modyfikowane:
; - zmienna licznikowa cnt
; - flagi Z, C
;
;PRZYKŁAD UŻYCIA
; ld A,#$E7
; ld liczba_a,A
; ld A,#$10 |
; ld liczba_b,A
; call div_ab
;*******************************************************
.div_ab
;inicjacja zmiennych
push A ;zapamiętanie akumulatora
clr iloraz ;część całkowita = 0
clr reszta ;reszta z dzielenia = 0
;sprawdzenie, czy liczba_a i liczba_b ≠ 0
ld A,liczba_b
jrugt dziel0 ;jeśli liczba_b ≠ 0, to sprawdzenie liczba_a
end_dziel
pop A ;koniec pracy podprogramu, odtworzenie akumulatora
ret
dziel0
ld A,number_a ;jeśli A=0, to wynik również = 0
jreq end_div ;jeśli A≠0, to wykonaj działania
;podprogram wykonujący dzielenie
rcf ;flaga C=0
ld A,#$08 ;inicjacja licznika przesunięć liczby
ld cnt,A
ld A,liczba_a
rlc A ;przesunięcie w lewo i zapamiętanie rezultatu
ld iloraz,A
dziel1
ld A,reszta
rlc A ;resztę z dzielenia w lewo, aby uwzględnić flagę C
ld reszta,A
sub A,liczba_b
jrc dziel2 ;kontynuacja pracy?
ld reszta,A
dziel2
ld A,iloraz
rlc A ;przesunięcie w lewo ilorazu
ld iloraz,A
dec cnt
jreq dziel3 ;jeśli licznik przesunięć=0, to koniec pracy
jra dziel1
dziel3
cpl A ;negowanie wyniku (ilorazu)
ld iloraz,A ;zapamiętanie ilorazu
jra end_dziel ;koniec pracy funkcji
Mnożenie całkowitych liczb 1-bajtowych bez znaku
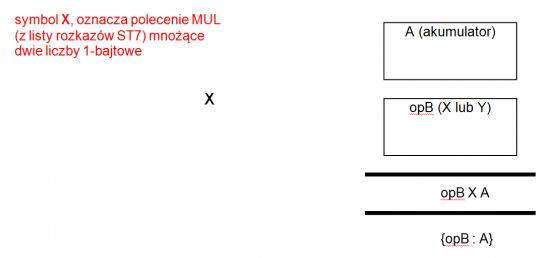
Prezentowany na listingu 2 podprogram mnoży przez siebie dwie liczby 1-bajtowe. ST7 zawiera na swojej liście rozkazów polecenie mnożenia dwóch liczb, jednak trzeba pamiętać o tym, że wynik mnożenia (iloczyn) może być liczbą 2-bajtową, inaczej niż czynniki. W związku z tym polecenie mnoży zawartość rejestru indeksowego X lub Y (opB) przez zawartość akumulatora (A), a wynik umieszcza w parze rejestrów: odpowiednio X i Y, lub Y i A. Akumulator zawiera mniej znaczący bajt iloczynu, natomiast rejestr indeksowy – bardziej znaczący. Uproszczony schemat funkcjonowania polecenia MUL umieszczono na rysunku 2.
Rysunek 2. Uproszczony schemat funkcjonowania polecenia MUL.
Listing 2. Podprogram mnożenia dwóch liczb 8-bitowych
;*******************************************************
;mnożenie liczba_a x liczba_b
;argumenty:
; - liczba_a, liczba_b (czynniki)
;rezultaty:
; - liczba_a (młodszy bajt iloczynu)
; - liczba_b (starszy bajt iloczynu)
;modyfikowane:
; - flagi H, C
;
;PRZYKŁAD UŻYCIA:
; ld A,#$A0
; ld liczba_a,A
; ld A,#$10
; ld liczba_b,A
; call mul_ab
;*******************************************************
.mul_AB
;zapamiętanie modyfikowanych rejestrów
push X
push A
;załadowanie zmiennych
ld X,liczba_A
ld A,liczba_B
mul X,A
ld liczba_a,A
ld liczba_b,X
;odtworzenie rejestrów
pop A
pop X
;powrót z podprogramu
ret
Mnożenie całkowitych liczb 2-bajtowych bez znaku
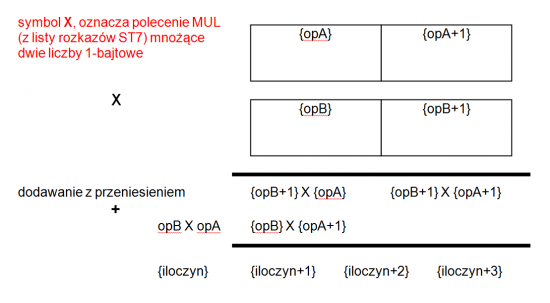
Prezentowany na listingu 3 podprogram mnoży przez siebie dwie liczby 2-bajtowe. Używane są operacje mnożenia liczb 8 bitowych oraz dodawania z przeniesieniem. Wynik mnożenia umieszczany jest w zmiennej iloczyn o długości 4 bajtów. Uproszczony schemat działania podprogramu zamieszczono na rysunku 3.
Rysunek 3. Uproszczony schemat działania podprogramu mnożącego 2 liczby 2-bajtowe.
Listing 3. Podprogram mnożenia dwóch liczb 2-bajtowych
;*******************************************************
;mnożenie liczba_a * liczba_b
;czynniki są 2-bajtowe, iloczyn jest 4-bajtowy
;argumenty:
; - liczba_a, liczba_b (czynniki)
;rezultaty:
; - 4-bajtowa zmienna iloczyn
;modyfikowane:
; - flagi C, Z
;
;PRZYKŁAD UŻYCIA:
; ld A,#$F3
; ld liczba_a,A
; ld A,#$D3
; ld {liczba_a+1},A
; ld A,#$FC
; ld liczba_b,A
; ld A,#$C3
; ld {liczba_b+1},A
; call mulw_ab
;*******************************************************
.mulw_ab
push A ;zapamiętanie na stosie modyfikowanych rejestrów
push X
ld X,liczba_b ;załadowanie liczb do mnożenia, bardziej znaczący
ld A,liczba_a ;bajt
mul X,A ;mnożenie liczb
ld iloczyn,X ;zapamiętanie iloczynu starszych bajtów
ld {iloczyn+1},A
ld X,{liczba_a+1} ;teraz mnożenie młodszych bajtów
ld A,{liczba_b+1}
mul X,A
ld {iloczyn+2},X ;zapamiętanie iloczynu młodszych bajtów
ld {iloczyn+3},A
ld X,liczba_a
ld A,{liczba_b+1} ;teraz mnożenie „na krzyż“ (patrz rysunek 3)
mul X,A
add A,{iloczyn+2} ;dodanie do poprzednio otrzymanych wartości
ld {iloczyn+2},A
ld A,X
adc A,{iloczyn+1}
ld {iloczyn+1},A
ld A,iloczyn
adc A,#0
ld iloczyn,A
ld X,liczba_b
ld A,{liczba_a+1} ;ponownie (następne bajty) mnożenie „na krzyż“
mul X,A
add A,{iloczyn+2} ;dodanie do poprzedniego wyniku
ld {iloczyn+2},A
ld A,X
adc A,{iloczyn+1}
ld {iloczyn+1},A
ld A,iloczyn
adc A,#0
ld iloczyn,A
pop X ;odtworzenie wartości rejestrów sprzed wywołania
pop A
ret ;koniec
Dzielenie całkowite liczby 4-bajtowej przez 2-bajtową
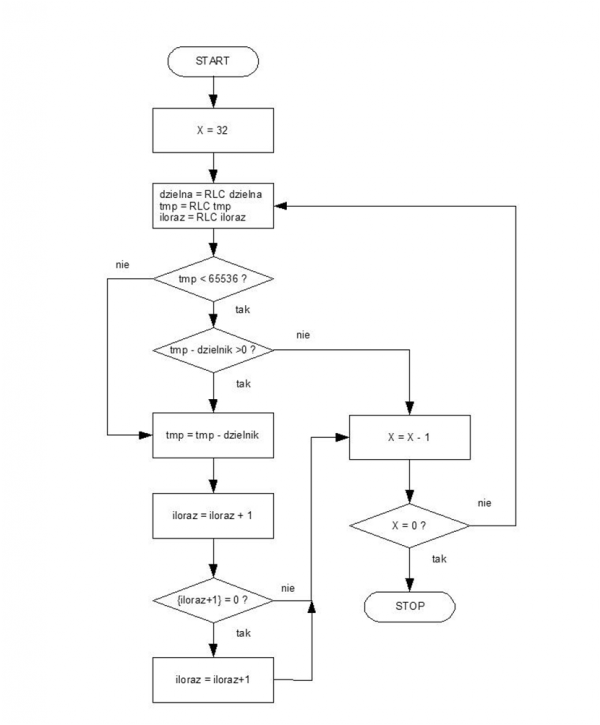
Na rysunku 4 przestawiono schemat podprogramu dzielenia liczby 4-bajtowej przez 2-bajtową. Iloraz otrzymany w wyniku dzielenia zapisywany jest w zmiennej 2 bajtowej, więc tak naprawdę funkcja znajdzie zastosowanie tylko w przypadkach, gdy iloraz jest mniejszy od 65536. Zmienne nazywają się tak, jak składniki operacji: dzielna, dzielnik, iloraz. Pozwoli to na ich łatwe rozróżnienie. Podprogram umieszczono na listingu 4.
Rysunek 4. Schemat podprogramu dzielenia liczby 4-bajtowej przez 2-bajtową
Listing 4. Podprogram dzielenia liczby 4-bajtowej przez 2-bajtową.
;*******************************************************
;Dzielenie liczby typu LONG przez liczbę typu WORD
;argumenty:
; - dzielna (4 bajty)
; - dzielnik (2 bajty)
;rezultaty:
; - 2-bajtowa zmienna iloraz
;modyfikowane:
; - flagi C, Z
; - wewnętrzna zmienna tmp
;
;PRZYKŁAD UŻYCIA:
; ld A,#$0E
; ld dzielna,A
; ld A,#$DC
; ld {dzielna+1},A
; ld A,#$BA
; ld {dzielna+2},A
; ld A,#$98
; ld {dzielna+3},A
; ld A,#$AB
; ld dzielnik,A
; ld A,#$CD
; ld {dzielnik+1},A
; call div_lw |
;*******************************************************
.div_lw
push A ;zapamiętanie rejestrów roboczych na stosie
push X
ld X,#32 ;inicjacja zmiennych
ld A,#0 ;instrukcja LD zajmuje więcej miejsca, niż CLR
ld iloraz,A ;jednak działa znacznie szybciej
ld {iloraz+1},A
ld tmp,A
ld {tmp+1},A
ld {tmp+2},A
ld {tmp+3},A
.wykonaj
sla {dzielna+3} ;przesunięcie dzielnej w lewo bez C
rlc {dzielna+2}
rlc {dzielna+1}
rlc dzielna
rlc {tmp+3} ;przesunięcie w lewo zmiennej pomocnicznej
rlc {tmp+2}
rlc {tmp+1}
rlc tmp
sla {iloraz+1} ;wynik nie może mieć więcej, niż 16 bitów, więc
rlc iloraz ;można przesuwać w prawo iloraz
ld A,tmp ;sprawdzenie, czy dzielna jest większa, czy równa
;od dzielnika
or A,{tmp+1}
jrne div_lw_odejmij
ld A,{tempquot+2}
cp A,divisor
jrugt divlw_odejmij
jrult divlw_bez_odejmowania
ld A,{tmp+3}
cp A,{dzielnik+1}
jrult divlw_bez_odejmowania
.divlw_odejmij ;odejmowanie dzielnika od dzielnej
ld A,{tmp+3}
sub A,{dzielnik+1}
ld {tmp+3},A
ld A,{tmp+2}
sbc A,dzielnik
ld {tmp+2},A
ld A,{tmp+1}
sbc A,#0
ld {tmp+1},A
ld A,tmp
sbc A,#0
ld tmp,A
inc {iloraz+1} ;zwiększenie ilorazu
jrne divlw_bez_odejmowania
inc iloraz
.divlw_bez_odejmowania
dec X ;zmniejszenie licznika „przejść“ pętli
jrne wykonaj ;jeśli licznik = 0,to koniec inaczej kontynuacja
pop X ;odtworzenie wartości rejestrów
pop A
ret ;koniec
Dodawanie dwóch liczb 2-bajtowych bez znaku
Dodawanie dwóch liczb bez znaku, nawet o dużej liczbie bajtów, jest bardzo proste. Wystarczy dodawać bajt po bajcie poczynając od najmłodszego bajtu, uwzględniając przeniesienie. Do zapamiętania wyniku dodawania wystarczająca jest taka liczba bajtów, jakiej jest długość najdłuższego ze składników i flaga przeniesienia. Dla opisywanego podprogramu są to dokładnie 2 bajty i flaga C (maksimum to $FFFF+$FFFF=$1FFFE, cyfra 1 może być reprezentowana przez flagę przeniesienia C). Podprogram umieszczono na listingu 5. Suma zapamiętywana jest w zmiennej sumaw, ale równie dobrze można wykorzystać do zapamiętania wyniku jeden ze składników.
Listing 5. Podprogram dodawania dwóch liczb 2-bajtowych bez znaku.
;*******************************************************
;Dodawanie 2 liczb 2-bajtowych bez znaku
;argumenty:
; - add_a (2 bajty)
; - add_b (2 bajty)
;rezultaty:
; - wynik zapamiętywany w sumaw
;modyfikowane:
; - flaga C
;
;PRZYKŁAD UŻYCIA:
; ld A,#$F3
; ld add_a,A
; ld A,#$D3
; ld {add_a+1},A
; ld A,#$FC
; ld add_b,A
; ld A,#$C3
; ld {add_b+1},A
; call addw
;*******************************************************
.addw
push A ;zapamiętanie rejestrów roboczych
push X
ld A,{add_a+1} ;pobranie młodszego liczby a
add A,{add_b+1} ;dodanie młodszego liczby b
ld {sumaw+1},A ;zapamiętanie młodszego bajtu sumy
ld A,add_a ;pobranie starszego bajtu liczby a
adc A,add_b ;dodanie przeniesienia i starszego bajtu liczby b
ld sumaw,A ;zapamiętanie starszego bajtu sumy
pop X ;odtworzenie rejestrów
pop A
ret
Odejmowanie dwóch liczb 2-bajtowych bez znaku
Przy odejmowaniu liczb o większej liczbie bajtów należy postępować dokładnie tak samo, jak w przypadku dodawania. Począwszy od najmłodszego bajtu odejmować z pożyczką bajt po bajcie. Rozmiar wyniku ponownie jest taki sam, jak długość najdłuższej liczby. Flaga przeniesienia sygnalizuje, czy odjemna jest większa odjemnika, czy też mniejsza. Przykładowy podprogram odejmowania umieszczono na listingu 6.
Listing 6. Podprogram odejmowania dwóch liczb 2-bajtowych bez znaku.
;*******************************************************
;Odejmowanie 2 liczb 2-bajtowych bez znaku
;argumenty:
; - sub_a (odjemna,2 bajty)
; - sub_b (odjemnik,2 bajty)
;rezultaty:
; - wynik zapamiętywany w roznicaw
;modyfikowane:
; - flaga C
;
;PRZYKŁAD UŻYCIA:
; ld A,#$F3
; ld sub_a,A
; ld A,#$D3
; ld {sub_a+1},A
; ld A,#$FC
; ld sub_b,A
; ld A,#$C3
; ld {sub_b+1},A
; call subw
;*******************************************************
.subw
push A ;zapamiętanie rejestrów roboczych
push X
ld A,{sub_a+1} ;pobranie młodszego liczby a
sub A,{sub_b+1} ;dodanie młodszego liczby b
ld {roznicaw+1},A ;zapamiętanie młodszego bajtu różnicy
ld A,sub_a ;pobranie starszego bajtu liczby a
sbc A,sub_b ;odjęcie przeniesienia i starszego bajtu liczby b
ld roznicaw,A ;zapamiętanie starszego bajtu roznicy
pop X ;odtworzenie rejestrów
pop A
ret
Sprawdzenie, czy liczba 2-bajtowa bez znaku mieści się w podanym zakresie
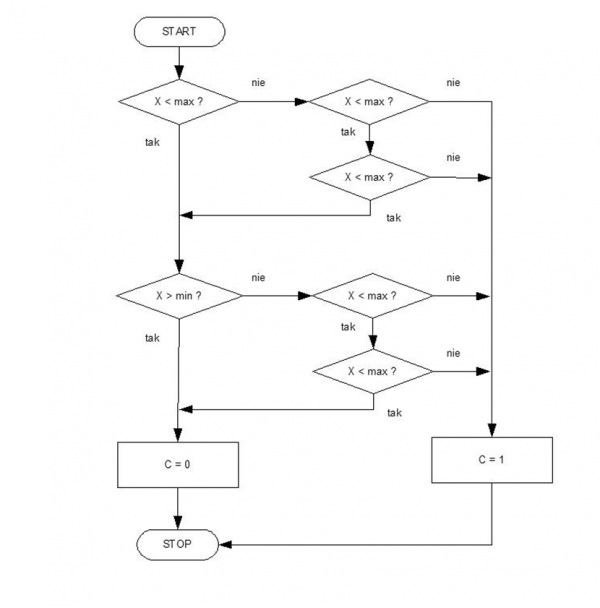
Podprogram sprawdza, czy liczba 2-bajtowa znajduje się w zadanym zakresie wartości. Zmienna data zawiera liczbę do przetestowania, zmienna min określa wartość minimalną a max – maksymalną. Stan flagi C po opuszczeniu podprogramu jest zależny od rezultatu testu. Wartość logiczna flagi C równa „0“ oznacza, że testowana zmienna mieści się w zakresie od min do max, natomiast wartość „1“ oznacza, że leży poza nim. Na rysunku 7 umieszczono schemat podprogramu testującego, natomiast listing 7 zawiera jego kod źródłowy.
Rysunek 5. Schemat podprogramu testującego, czy zmienna leży w zakresie od min do max
Listing 7. Podprogram testujący, czy liczna mieści się w zakresie od min do max
;*******************************************************
;Testowanie, czy zmienna (data > min) i (data < max)
;argumenty:
; - data (2 bajty,testowana liczba)
; - min (wartość minimalna,2 bajty)
; - max (wartość maksymalna, 2 bajty)
;rezultaty:
; - C=0, gdy min < data < max inaczej C=1
;modyfikowane:
; - flaga C
;
;PRZYKŁAD UŻYCIA:
; ld A,#$25
; ld data,A
; ld A,#$00
; ld {data+1},A
; ld A,#$00
; ld min,A
; ld A,#$C3
; ld {min+1},A
; ld A,#$CC
; ld max,A
; ld A,#$05
; ld {max+1},A
; call check_min_max
;*******************************************************
.check_min_max
push A ;zapamiętanie rejestrów roboczych
push X
ld X,data ;pobranie do X bardziej znaczącego bajtu do testu
ld A,{data+1} ;pobranie do A mniej znaczącego bajtu
cp X,max ;porównanie bardziej znaczącego bajtu z max (maksimum)
jrugt out_of_range ;jeśli większy, to wyjście
jrne comp_min ;jeśli równy, to porównanie mniej znaczącego bajtu
cp A,{max+1}
jrugt out_of_range ;mniej znaczący bajt większy - wyjście
comp_min
cp X,min ;to samo dla wartości minimalnej min
jrult out_of_range
jrne in_range
cp A,{min+1}
jrult out_of_range
in_range
rcf ;zmienna mieści się w zakresie – C=0
jra check_exit
out_of_range
scf ;zmienna poza zakresem – C=1
check_exit
pop X ;odtworzenie rejestrów roboczych
pop A
ret
Sprawdzenie odchylenia od środkowej liczby 2-bajtowej
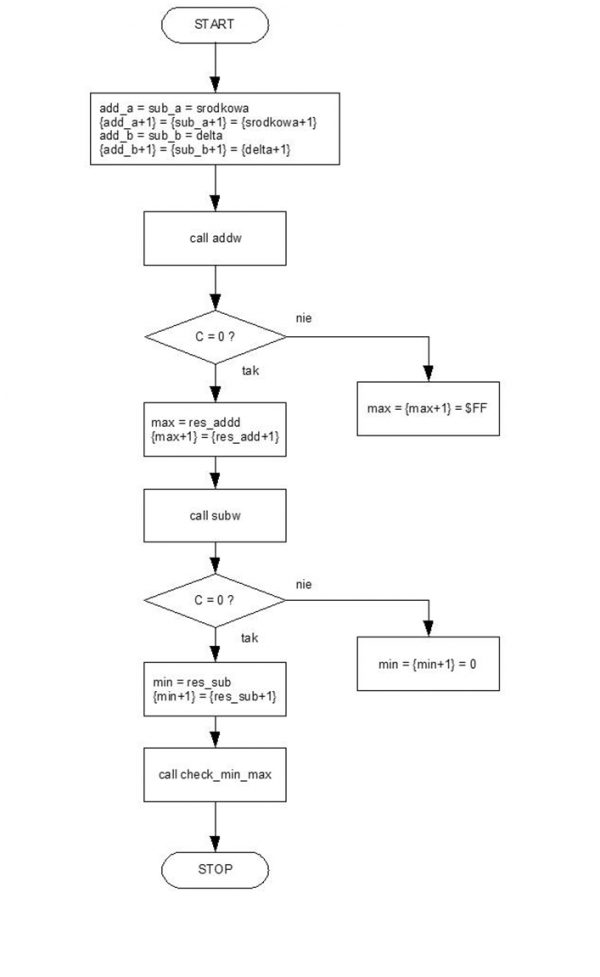
Funkcjonalnie podprogram jest bardzo zbliżony do poprzednio prezentowanego. Poprzedni testował, czy zmienna mieści się w zakresie min – max, ten sprawdza – po podaniu parametrów: środkowa, delta (odchylenie) i zmiennej data – czy zmienna nie przekracza zadanego odchylenia delta. Podprogram kończy pracę sygnalizując rezultat testu przy pomocy flagi przeniesienia C. Gdy ta jest ustawiona, to zmienna przekracza zadane odchylenie, natomiast gdy jest zerem, to zmienna mieści się w zakresie srodkowa-delta < data < srodkowa+delta.
Rysunek 6. Schemat podprogramu testującego, czy zmienna mieści się w zakresie odchyłki środkowa ± Δ
Listing 8. Podprogram sprawdzający, czy zmienna mieści się w zakresie środkowa ± Δ
;*******************************************************
;Testowanie, czy zmienna (data > środkowa-delta)
;i (data < środkowa+delta)
;argumenty:
; - data (2 bajty,testowana liczba)
; - delta (wartość odchylenia,2 bajty)
; - srodkowa (wartość środkowa, 2 bajty)
;rezultaty:
; - C=0, gdy zmienna nie przekracza odchylenia, inaczej C=1
;modyfikowane:
; - flaga C
;
;PRZYKŁAD UŻYCIA
; ld A,#$25
; ld data,A
; ld A,#$00
; ld {data+1},A
; ld A,#$00
; ld delta,A
; ld A,#$23
; ld {delta+1},A
; ld A,#$CC
; ld srodkowa,A
; ld A,#$05
; ld {srodkowa+1},A
; call check_range
;*******************************************************
.check_range
push X ;zapamiętanie rejestrów roboczych
push A
ld A,srodkowa ;pobranie starszego bajtu wartości środkowej
ld add_a,A ;i zapamiętanie jej w zmiennych add_a i sub_a
ld sub_a,A ;dla podprogramów addw i subw
ld A,{srodkowa+1} ;to samo dla młodszego bajtu
ld {add_a+1},A
ld {sub_a+1},A
ld A,delta ;to samo dla delta, ale w zmiennych add_b i sub_b
ld add_b,A
ld sub_b,A
ld A,{delta+1}
ld {add_b+1},A
ld {sub_b+1},A
call addw ;obliczenie sumy srodkowa + delta
jrnc no_ovfmax ;jeśli przekroczono zakres,to ustaw wartość MAX na
ld A,#$FF ;$FFFF (maksymalna dla 2 bajtów)
ld max,A
ld {max+1},A
no_ovfmax
ld A,res_add ;jeśli nie ma przekroczenia zakresu, to wówczas
ld max,A ;za maksimum przyjmij wyliczoną wartość
ld A,{res_add+1}
ld {max+1},A
call subw ;obliczenie wartości srodkowa-delta
jrnc no_ovfmin ;jeśli wystąpiło przeniesienie, to wartość minimum
clr A ;ustaw na 0
ld min,A
ld {min+1},A
no_ovfmin
ld A,res_sub ;jeśli nie ma przeniesienia,to za minimum przyjmij
ld min,A ;wyliczoną w wyniku odejmowania wartość
ld A,{res_sub+1}
ld {min+1},A
call check_min_max ;wywołaj podprogram i sprawdź, czy zmienna jest w
;zakresie ustalonym przez MIN i MAX
pop A ;odtworzenie rejestrów roboczych
pop X
ret
Konwersja liczb binarnych na dziesiętne
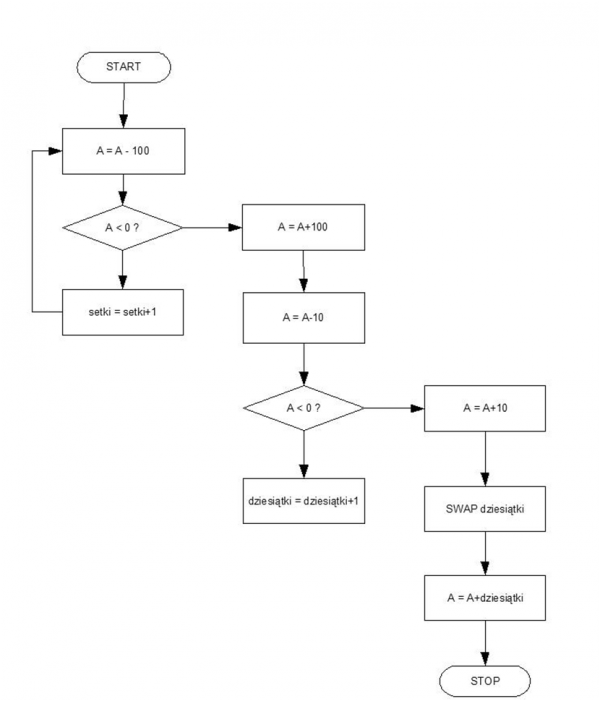
Podprogram wykonuje konwersję liczby binarnej bez znaku zawartej w akumulatorze, to jest z zakresu od 0 do 255, na liczbę dziesiętną. Po zakończeniu zmienne setki idziesiatki zawierają wartości w kodzie BCD otrzymane w wyniku konwersji (zmienna setki zawiera cyfrę setek, zmienna dziesiatki cyfry dziesiątek i jedności). Schemat funkcjonowania podprogramu umieszczono na rysunku 9, a listing 9 zawiera jego kod źródłowy.
Rysunek 7. Schemat podprogramu konwersji liczby binarnej na dziesiętną
Listing 9. Konwersja liczby 1-bajtowej w kodzie binarnym na dziesiątną
;*******************************************************
;Konwersja liczby 1-bajtowej, binarnej na dziesiętną
;argumenty:
; - liczba w akumulatorze
;rezultaty:
; - setki: cyfra setek
; - dziesiątki: cyfra dziesiątek i jednostek
;modyfikowane:
; - flaga C, Z, zmienne wyniku
;
;PRZYKŁAD UŻYCIA
; ld A,#$D4
; call BtoD
.BtoD
clr setki ;inicjacja zmiennych
clr dziesiatki
hund
sub A,#100 ;A = A - 100
jrc ten ;sprawdzenie, czy A < 100
inc hundreds ;jeśli nie, to zwiększanie licznika setek
jra hund ;pętla do spełnienia w/w warunku
ten
add A,#100 ;dodanie 100, aby uzupełnić A po ostatniej operacji
temp ;(nastąpiło przekroczenie zakresu)
sub A,#10 ;A = A - 10
jrc unit ;jak w przypadku setek – sprawdzenie, czy A < 10
inc tens ;i jeśli nie, to zwiększanie licznika 10-tek
jra temp ;pętla do spełnienia w/w warunku
unit
add A,#10 ;dodanie 10, aby uzupełnić A po ostatnim odejmowaniu
swap tens ;zamiana połówek bajtu tak, aby bardziej znaczący bajt
;zawierał cyfrę dziesiątek
or A,tens ;dodanie jednostek (A zawiera jednostki po odejmowaniu
ld tens,A ;setek i dziesiątek)
ret






Dodaj nowy komentarz